
작성일시: 2023년 8월 2일 오후 1:17
📖Problems: #15486. 퇴사2
15486번: 퇴사 2
첫째 줄에 N (1 ≤ N ≤ 1,500,000)이 주어진다. 둘째 줄부터 N개의 줄에 Ti와 Pi가 공백으로 구분되어서 주어지며, 1일부터 N일까지 순서대로 주어진다. (1 ≤ Ti ≤ 50, 1 ≤ Pi ≤ 1,000)
www.acmicpc.net
등급 : 골드 V
- 백준이가 퇴사 하려고 함
- N+1일째 되는 날 퇴사 하기 위해, 남은 N일동안 최대한 많은 상담을 하려고 함. 이때 백준이가 얻을 수 있는 최대 수익을 구하는 프로그램을 작성하시오
- 각 상담은 ‘상담을 완료하는데 걸리는 시간 Ti’와 상담을 했을 때 받을 수 있는 금액 Pi로 이루어짐
- example: N = 7퇴사 전 할 수 있는 상담의 최대 이익은 1일, 4일, 5일에 상담하는 거이며, 이때의 이익은 10+20+15=45이다.

 |
 |
 |
 |
🔍Process
💡 약 1일동안 게속 고민했던 문제였고, 어떻게 삽질했는지 정리하면 너무 많아질 것 같아 어떤 순서로, 정답을 찾아가게 되었는지를 정리하려고 한다.
🔍문제를 보고 나서 생각나는 유형은?
- Dynamic Programming
- ‘최대 수익’을 구해야 하는 것과 테이블 형식이 주어졌다는 것을 힌트 삼았다.
Dynamic Programming
- 큰 문제를 작은 문제로 나누어 푸는 문제로, 작은 문제가 반복된다.
- (분할정복은 큰 문제를 해결하기 어려워 작은 문제로 나누어 품)
- 조건 : 작은 문제가 반복이 일어남. 같은 문제는 구할 때마다 정답이 같음!!
🔍이 문제에 필요한 DP
- DP의 크기는?
dp=[0]*(n+1)i 0 1 2 3 … n dp[i] 0 0 0 0 0 0 - 이 부분에서 헷갈려서
(n+1)*(n+1)크기의 테이블을 만들기도 했었는데, 하나하나 대입하다 보니까 최댓값만 dp에 저장하는 것이므로 굳이(n+1)*(n+1)을 할 필요가 없다고 느꼈다.
- dp에 저장하는 조건:
- day가 주어진 N을 넘지 않을 때 저장
- 해당 날짜(
day)의 위치에 저장
필요한 변수&리스트
n: 남은 날짜t[]: time 리스트 (0~n+1)p[]: pay리스트 (0~n+1)day:i(현재) + t[i] - 1, 현재 값에서 t[i]의 값을 더한 일을 마무리하는 날
💡 DP문제에서 중요한 것은 점화식이다. 어떤 규칙이 반복되는지 직접 살펴보자.
주어진 조건은 day가 N을 넘지 않는 것이므로, 아래와 같이 표현할 수 있다.
if day <= n:
dp[day] = ?먼저 dp에 어떻게 저장 시킬 지에 대해서 코드와 관련없이 “인간”이라면 어떤 방식으로 저장시킬지 생각해보도록 한다.
예제는 예제1을 사용하도록 한다.

우선 dp[day]일 때 pay의 값을 저장한다고 가정한 후, 동작 과정을 살펴보자.
i = 1
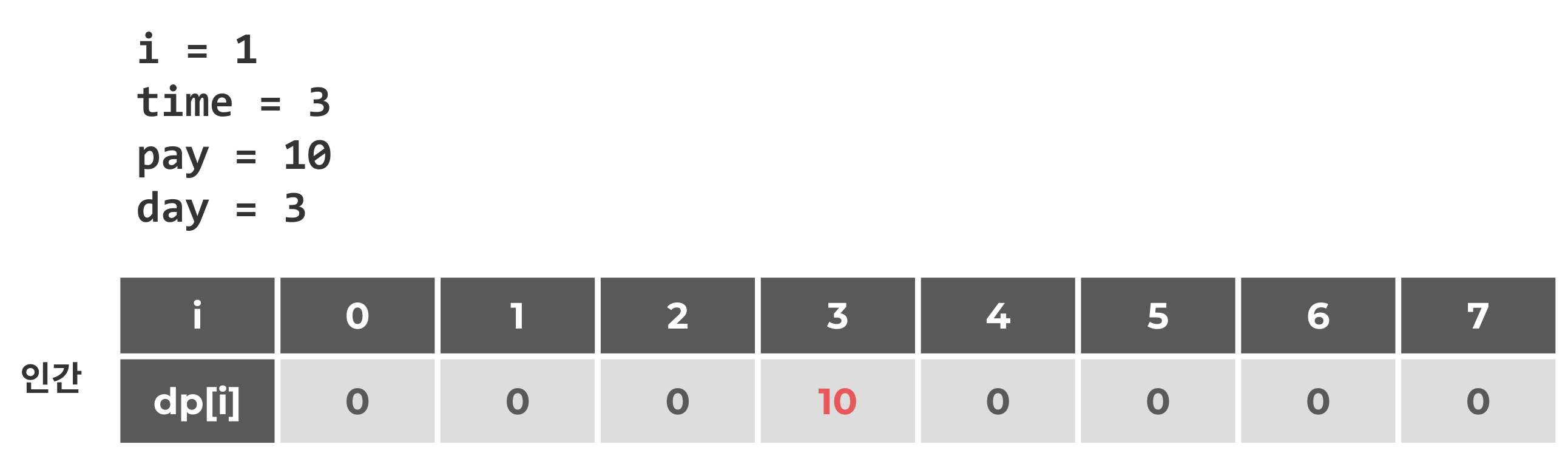
i = 2
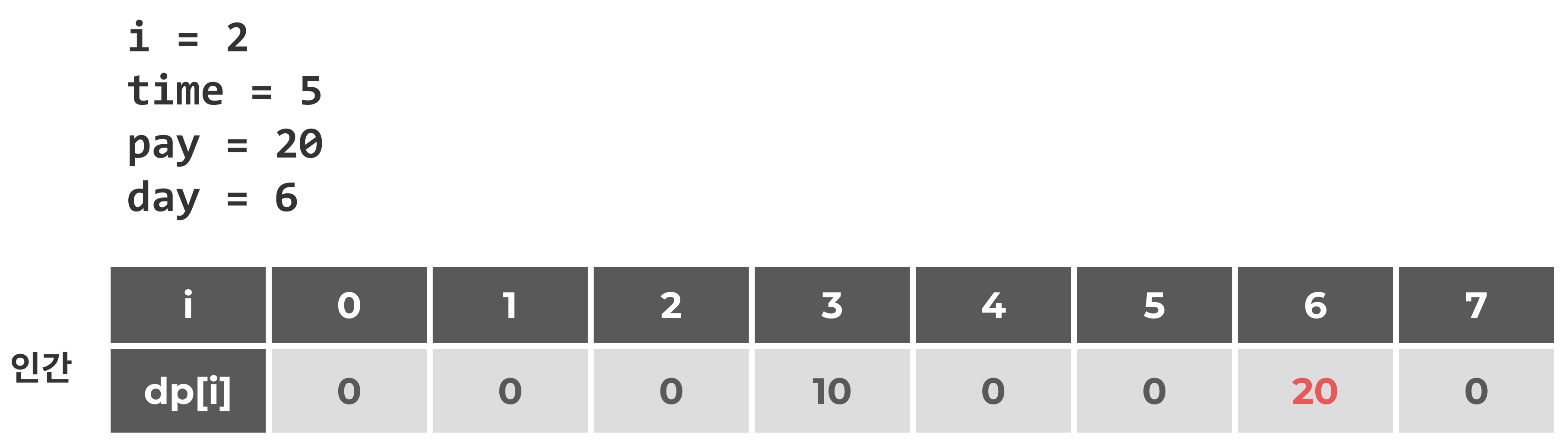
i = 3
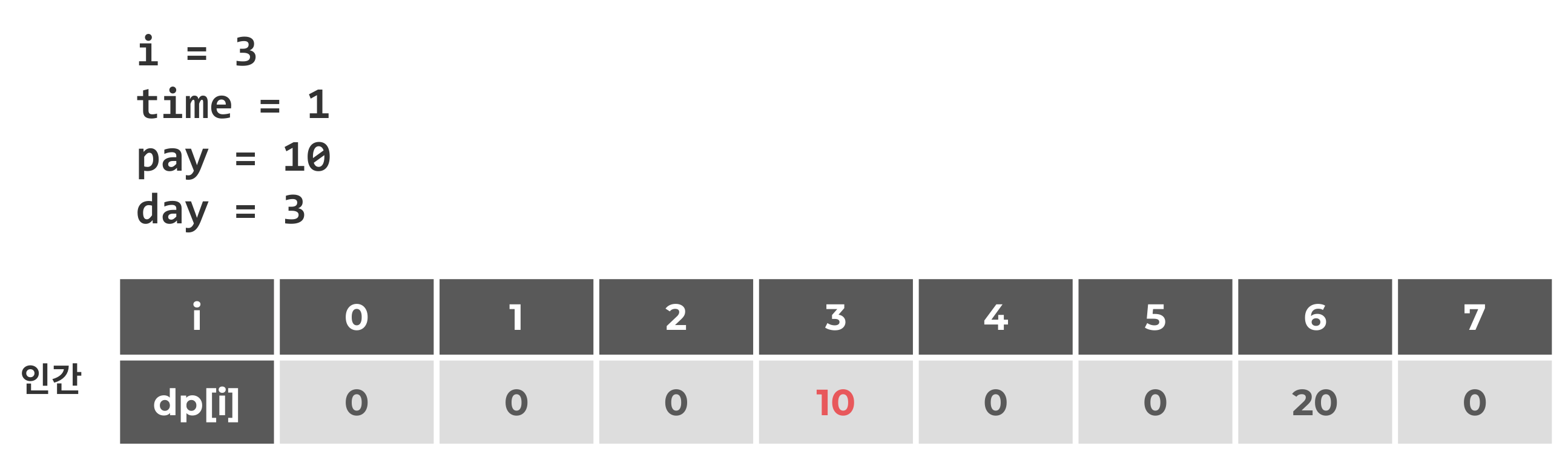
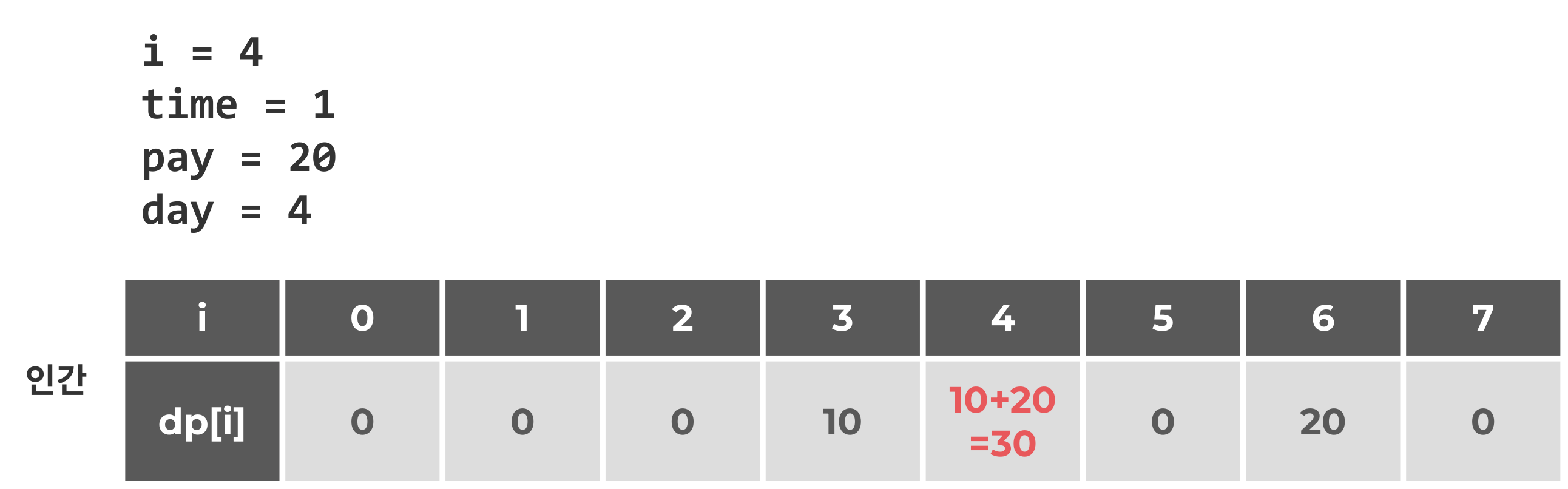
i = 4일때 그냥 day[4]에 pay값을 저장해버린다면, 어떻게 되는지 살펴보자.
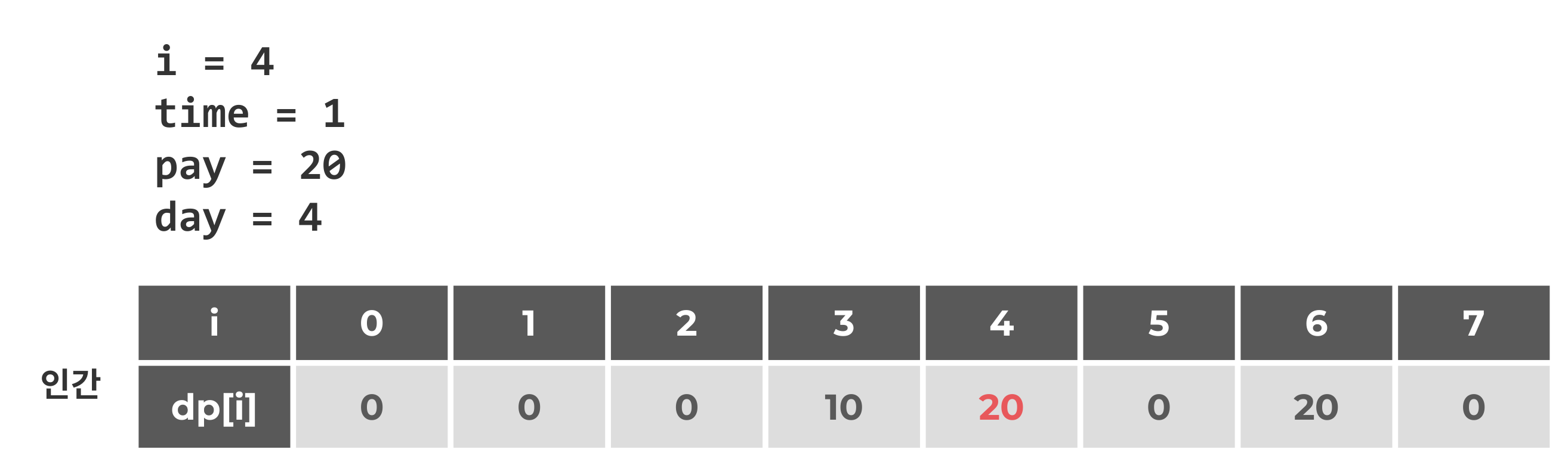
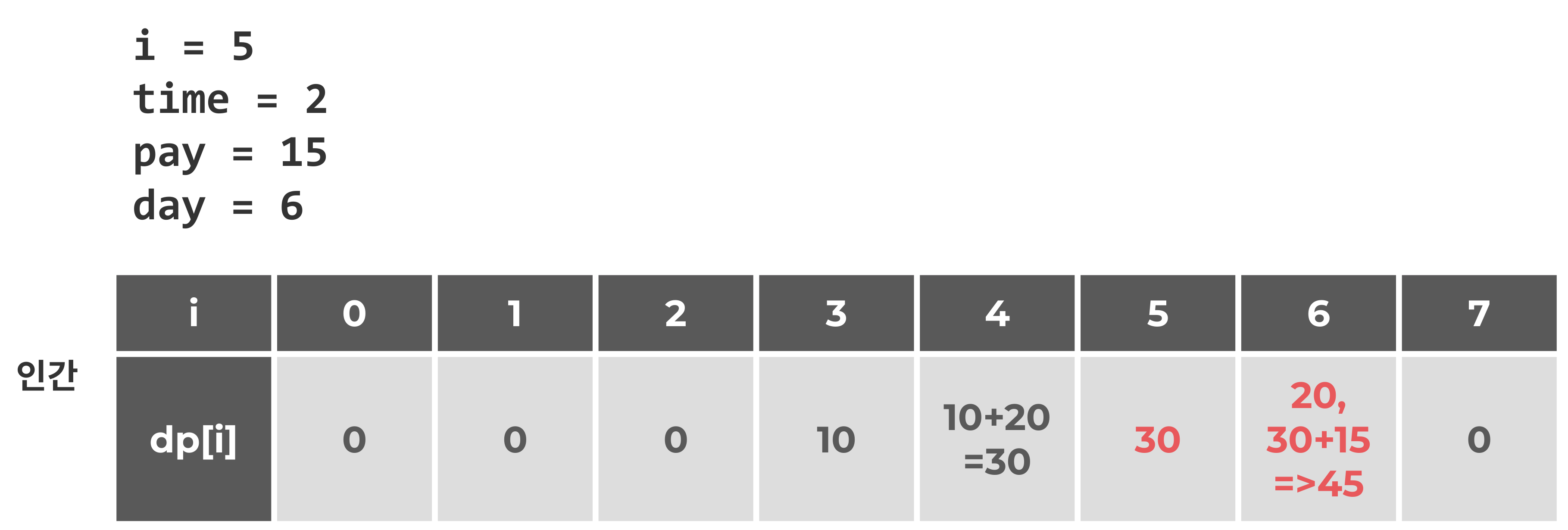
i = 5
또한, i=5에서 dp[6]에 저장되어야 하는데 이때 기존에 있던 20과 새로 저장하는 15 중에 20을 저장해야 한다. 왜냐하면 dp에는 더 큰 값이 들어가야 하기 때문이다. 따라서 이를 비교하는 항목도 필요하다. (dp[day] = max(dp(day), pay)

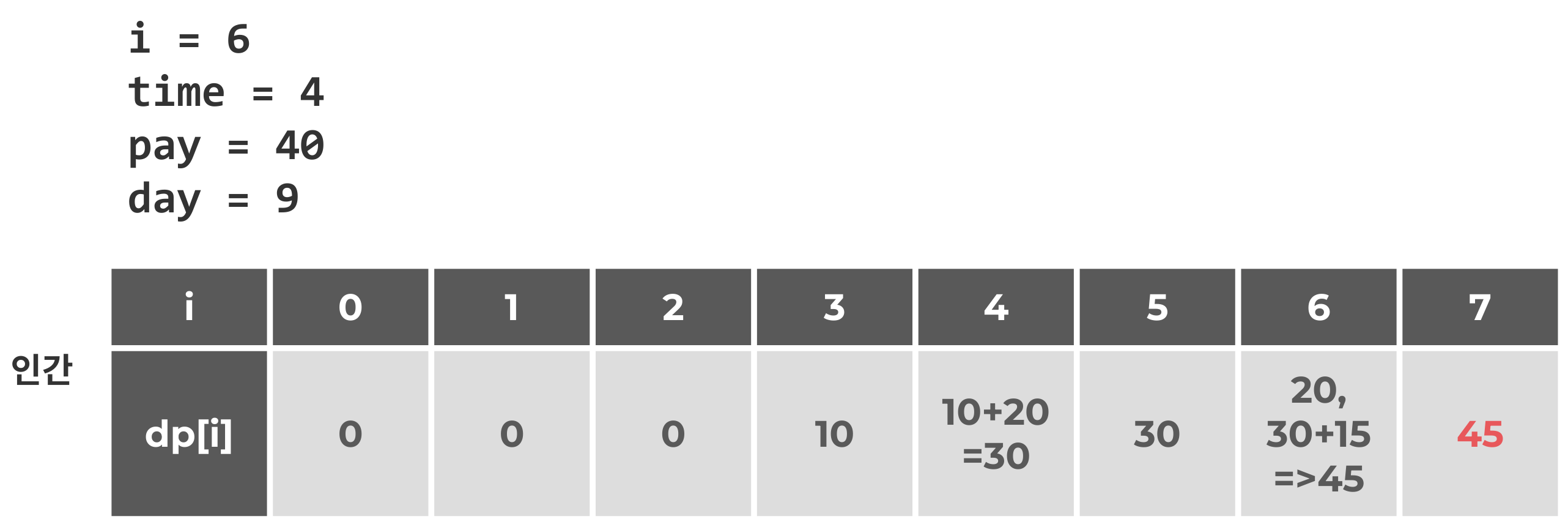
어차피 i = 6, i = 7에서는 day값이 N을 넘어가니 여기까지 보도록 한다.
이때 이 예제의 정답은 45임에도 불구하고, 최종적으로 담긴 것은 15이며, dp에서 가장 큰 값은 20이 된다. 이는 그냥 pay만 저장하면 안 된다는 것을 의미한다. 즉, i=4가 저장될 때 i=3에 있던 값을 더해주며 저장해야 한다.(dp[day] = max(dp[day], dp[i-1]+pay) 다시 인간적으로 생각했을 때 어떻게 되어야 하는지 보자.
이때, i=5일때 dp[5]에 저장되는 값이 없으므로, dp[5]에 값에도 30이 저장되어야 한다.
이후, i=6, i=7은 조건(day ≤ N)에 만족하지는 않지만 이전 값을 그대로 가져오는게 필요하다.
i = 6
i = 7
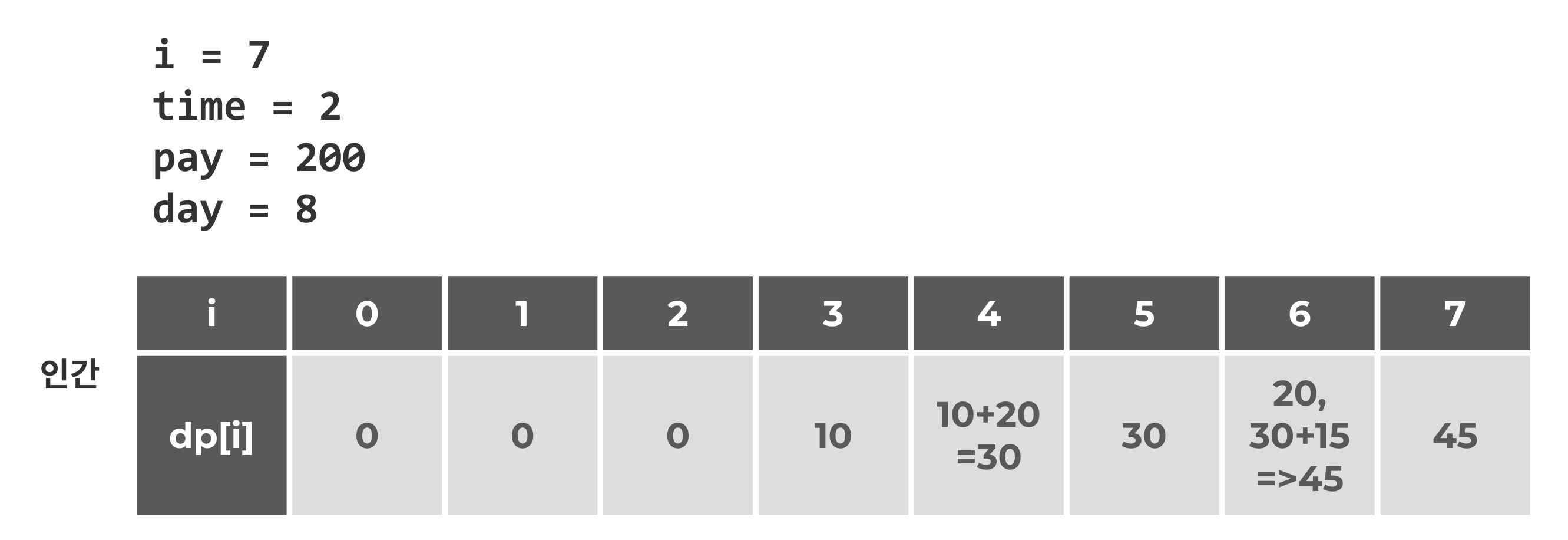
인간적으로 볼 때에는 이러한 로직으로 구성되는 것이 가장 이상적이다. 이때, 중간중간 필요한 부분들이 있었다.
- i=5에서 dp[6]에 저장되어야 하는데 이때 기존에 있던 20과 새로 저장하는 15 중에 20을 저장해야 한다. 왜냐하면 dp에는 더 큰 값이 들어가야 하기 때문이다. 따라서 이를 비교하는 항목도 필요하다.
⇒ 비교하기 위해 max함수로 비교한다. 이미 저장되어 있는 값과 pay값 중 큰 값을 다시 저장한다.dp[day] = max(dp(day), pay - i=4가 저장될 때 i=3에 있던 값을 더해주며 저장해야 한다.
⇒ 이전 값을 더한 값과 원래 있던 값을 비교해야 한다. (dp[day] = max(dp[day], dp[i-1]+pay) - 이후, i=6, i=7은 조건(day ≤ N)에 만족하지는 않지만 이전 값을 그대로 가져오는게 필요하다.
⇒ 조건문에 들어가기 전에, 이전까지의 최대값을 미리 현재 위치에 대입을 해줘야 한다. 이때 현재 값이 더 클 수도 있기 때문에 이미 있는 값과 그 전 값 중에서 큰 값을 저장한다.dp[i] = max(dp[i], dp[i-1]

로직을 어느정도 정립을 했으니, 이상적으로 잘 돌아가는지 확인해보도록 한다. 빨간색문장은 빨간색으로 저장을 하고, 파란색 조건문 수행 결과는 파란색으로 저장하였다.
i = 1

조건(day <= n) 에 만족하므로,
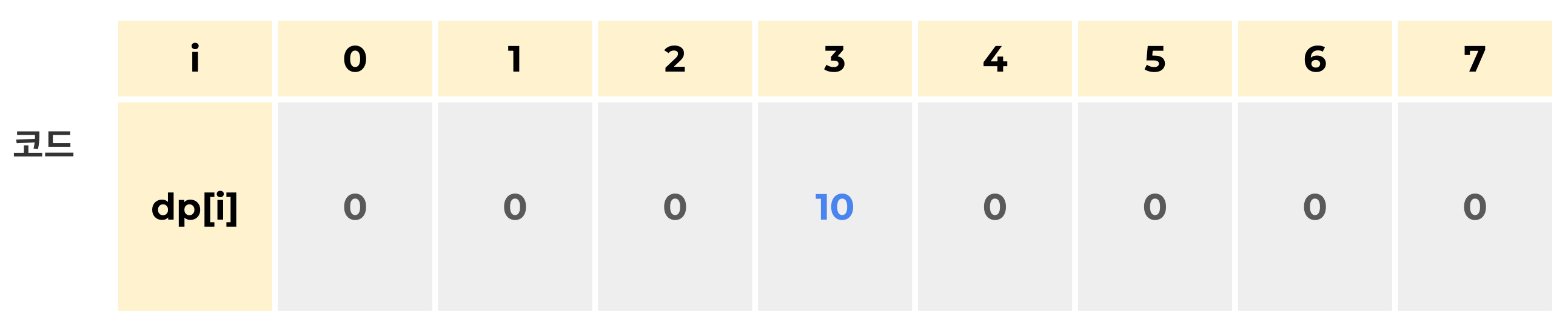
i = 2

조건(day <= n) 에 만족하므로,
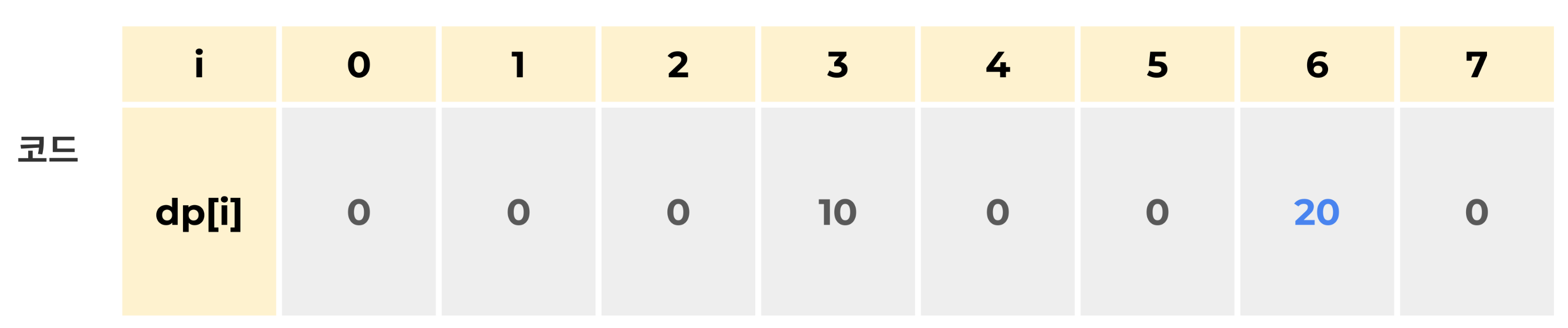
i = 3

조건(day <= n) 에 만족하므로,
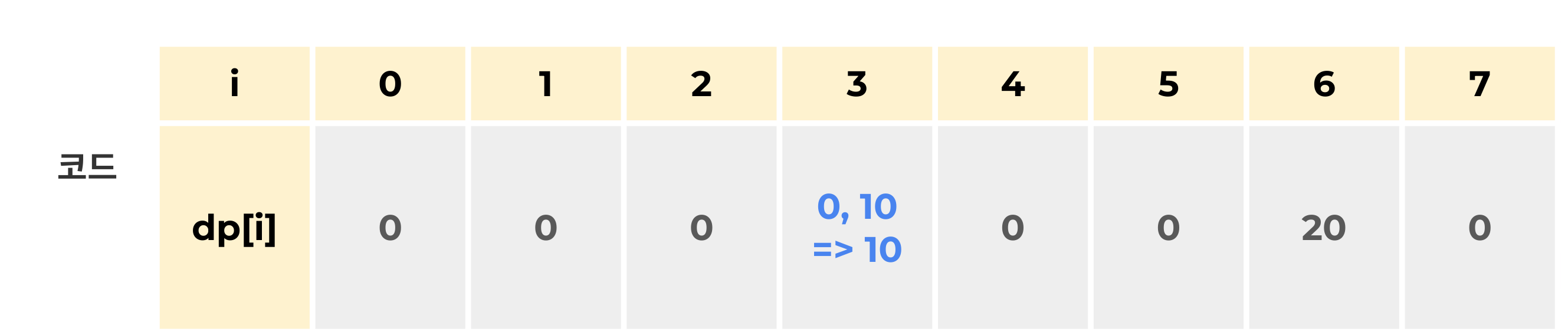
i = 4

조건(day <= n) 에 만족하므로,

i = 5

조건(day <= n) 에 만족하므로,
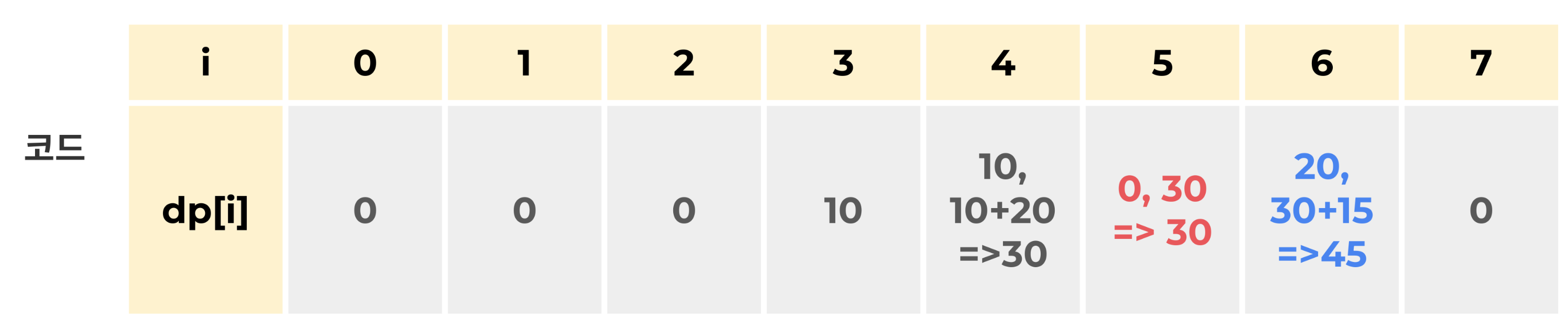
i = 6

조건에 만족하지 않으므로, 조건문은 실행하지 않는다.
i = 7

조건에 만족하지 않으므로, 조건문은 실행하지 않는다.
로직이 우리가 원하는대로 정상적으로 돌아가는 것을 확인했다.
따라서 아래와 같이 코드를 구체화할 수 있다. 매번 pay와 time의 값이 i가 바뀔 때마다 달라져야 한다.
for i in range(1, n+1):
time = t[i]
pay = p[i]
day = i + time - 1
dp[i] = max(dp[i], dp[i - 1])
if day <= n:
dp[day] = max(dp[day], dp[i-1]+pay)
print(max(dp))입력받는 것은 sys를 이용해야 시간초과가 뜨지 않는다. 입력받는 것까지 코드를 짠 최종코드는 아래와 같다.
import sys
input = sys.stdin.readline
n = int(input()) # 수 입력 받기
t, p = [0 for _ in range(n + 1)], [0 for _ in range(n + 1)]
for i in range(1, n + 1):
t[i], p[i] = map(int, input().split())
dp = [0] * (n+1) #dp 리스트 초기화
for i in range(1, n+1):
time = t[i]
pay = p[i]
day = i + time - 1
dp[i] = max(dp[i], dp[i - 1]) # 이전까지의 최댓값
if day <= n:
dp[day] = max(dp[day], dp[i-1]+pay)
print(max(dp))-> 이후 다른 예제도 정상적으로 작동하는지 확인해야 한다. (나의 경우, 이렇게 정리하기 전에는 코드를 잘못 짜서 예제 3에서 계속 오류가 났었다.)
🚩My submission
import sys
input = sys.stdin.readline
n = int(input()) # 수 입력 받기
t, p = [0 for _ in range(n + 1)], [0 for _ in range(n + 1)]
for i in range(1, n + 1):
t[i], p[i] = map(int, input().split())
dp = [0] * (n+1) #dp 리스트 초기화
for i in range(1, n+1):
time = t[i]
pay = p[i]
day = i + time - 1
dp[i] = max(dp[i], dp[i - 1]) # 이전까지의 최댓값
if day <= n:
dp[day] = max(dp[day], dp[i-1]+pay)
print(max(dp))🚩Others submission
import sys
input = lambda: sys.stdin.readline().rstrip()
n = int(input())
t, p = [0 for _ in range(n + 1)], [0 for _ in range(n + 1)]
for i in range(1, n + 1):
t[i], p[i] = map(int, input().split())
dp = [0 for _ in range(n + 1)]
for i in range(1, n + 1):
dp[i] = max(dp[i], dp[i - 1]) # 이전까지의 최댓값
fin_date = i + t[i] - 1 # 당일 포함
if fin_date <= n: # 최종일 안에 일이 끝나는 경우
# i일부터는 일을 해야하므로 i일에 얻을 수 있는 최댓값이 아닌 i-1일까지 얻을 수 있는 최댓값을 구한다
dp[fin_date] = max(dp[fin_date], dp[i - 1] + p[i])
print(max(dp))-
import sys
input = sys.stdin.readline
n = int(input())
t,p = [],[]
dp = [0] * (n+1)
for i in range(n):
x,y = map(int,input().split())
t.append(x)
p.append(y)
M = 0
for i in range(n):
M = max(M,dp[i])
if i+t[i] > n :
continue
dp[i+t[i]] = max(M+p[i],dp[i+t[i]])
print(max(dp))-
import sys
n = int(sys.stdin.readline())
t = [] # 각 상담을 완료하는데 걸리는 기간
p = [] # 각 상담을 완료했을 때 받을 수 있는 금액
# i번째 날부터 마지막 날까지 낼 수 있는 최대 이익
dp = [0] * (n+1)
for _ in range(n):
# 날짜별 상담 완료 기간 및 상담 완료 금액 저장
x, y = map(int, sys.stdin.readline().split(" "))
t.append(x)
p.append(y)
# i번째 날부터 마지막 날까지 낼 수 있는 최대 이익
max_value = 0
# 마지막 날짜부터 역순으로 탐색
for i in range(n-1, -1, -1):
# 해당 날짜에 상담을 진행할 수 있다면
if (i + t[i] <= n):
# [현재 상담 일자의 이윤 + 현재 상담을 마친 일자부터의 최대 이윤]과
# 현재 날짜부터 마지막 날까지 낼 수 있는 최대 금액을 비교
dp[i] = max(p[i] + dp[i + t[i]], max_value)
max_value = dp[i]
# 해당 날짜에 상담을 진행할 수 없다면
else:
dp[i] = max_value
print(max_value)💡TIL
- DP 문제는 처음부터 하나하나 핸드트레이싱 하는 게 답이다. 이상적으로 어떻게 하는게 맞는지 생각을 한 후, 그에 맞는 코드 풀이 방식을 대입해보면서 맞게 잘 수행하는지 트레이싱해야 한다.
- 이 문제는 아이디어를 얻기까지 상당한 삽질을 하였는데, 덕분에 dp 몸풀기 제대로 했다.
'🧑💻Problem Solutions > BOJ' 카테고리의 다른 글
| [BOJ] #3040. 백설공주와 일곱난쟁이들 (파이썬/Python) (0) | 2023.09.08 |
|---|---|
| [BOJ] #10844. 쉬운 계단의 수 (파이썬/Python) (2) | 2023.09.07 |
| [백준] #2607. 바이러스 (Python) (0) | 2023.07.25 |
| [백준] #10799. 쇠막대기 (Python) (0) | 2023.07.07 |
| [백준] #14888. 연산자 끼워넣기 (Python) (0) | 2022.10.30 |



