
작성일시: 2023년 8월 22일 오후 4:13
📖Problem : #70. Climbing Stairs
Climbing Stairs - LeetCode
Can you solve this real interview question? Climbing Stairs - You are climbing a staircase. It takes n steps to reach the top. Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top? Example 1: Input: n = 2 Outpu
leetcode.com
등급: Easy

- 계단을 오르고 있다. 꼭대기에 도달하기 위해서는 “n”개의 계단이 필요하다.
- 매번 한 계단 or 두 계단씩 오를 수 있다.
- 꼭대기까지 가기 위한 방법이 몇 가지인가?


🔍Institution
n = 1부터 한번 경우의 수를 나열해보자.

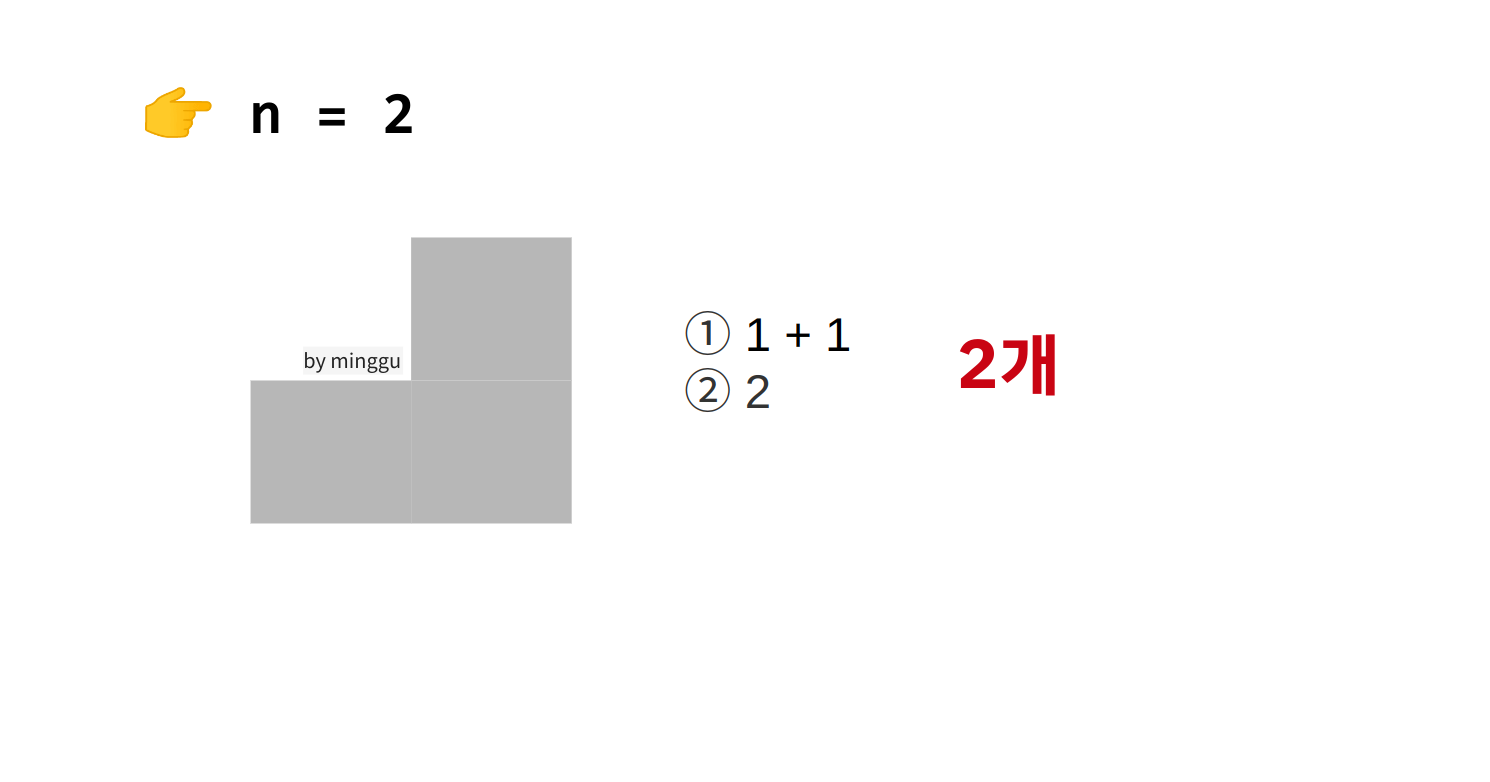

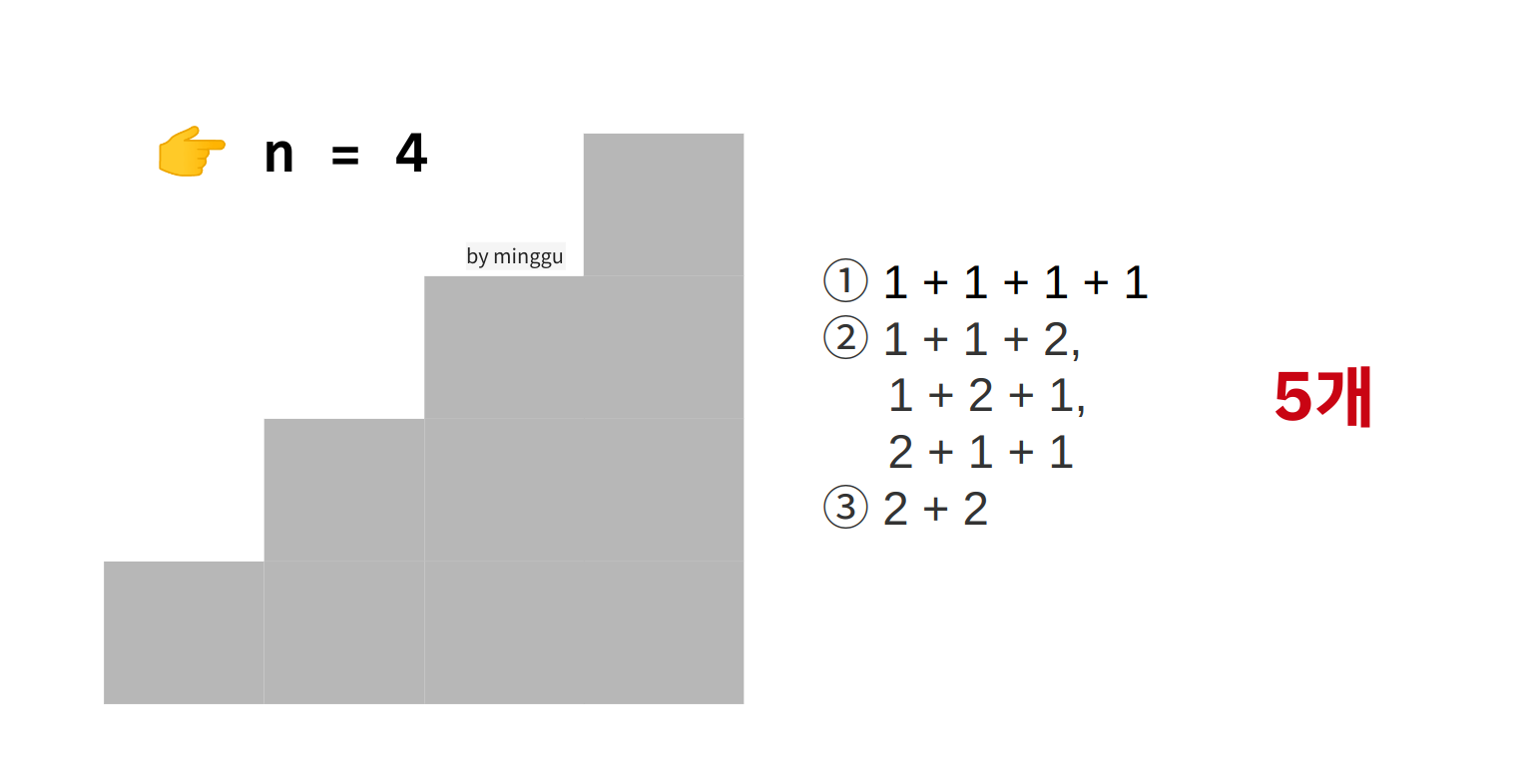
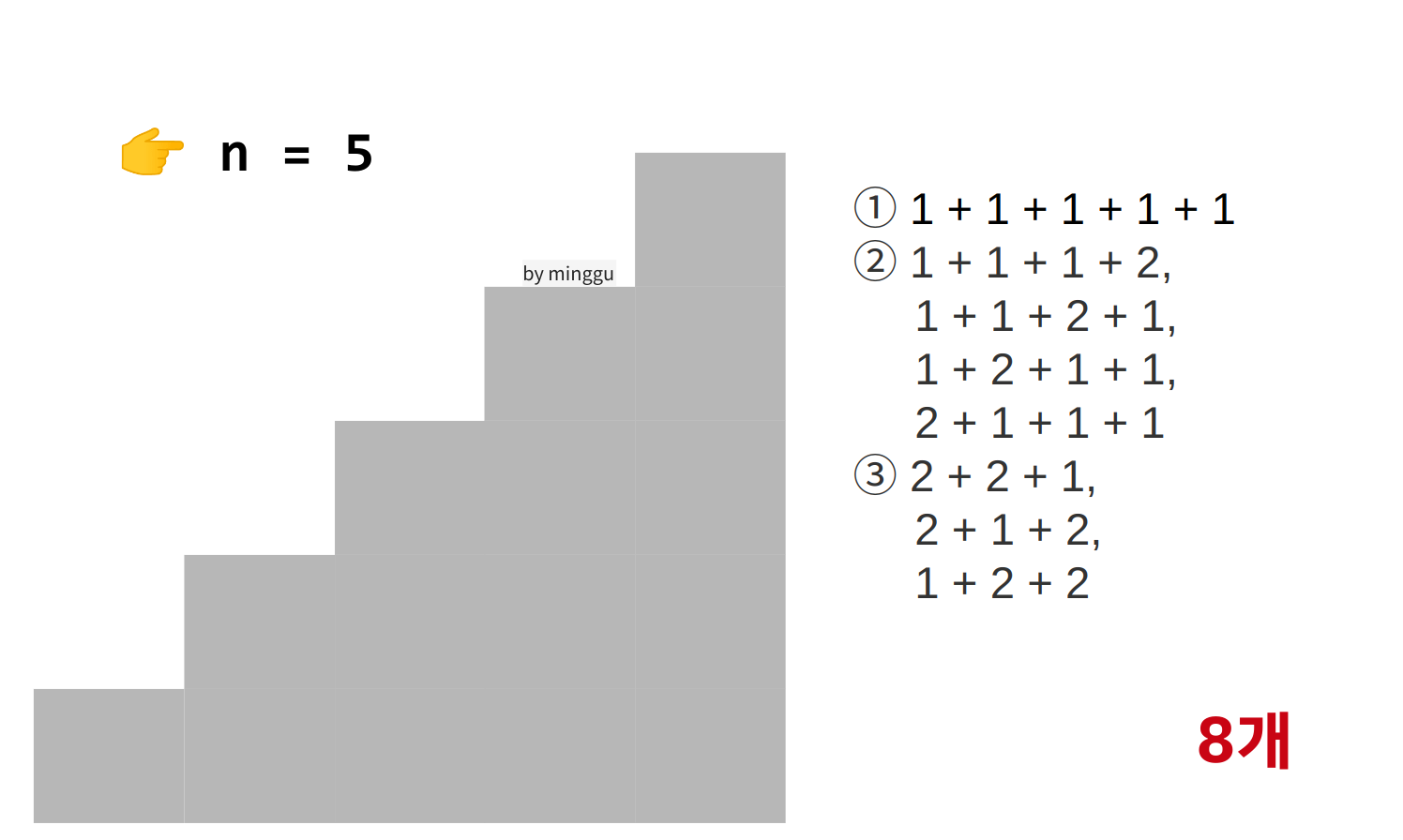
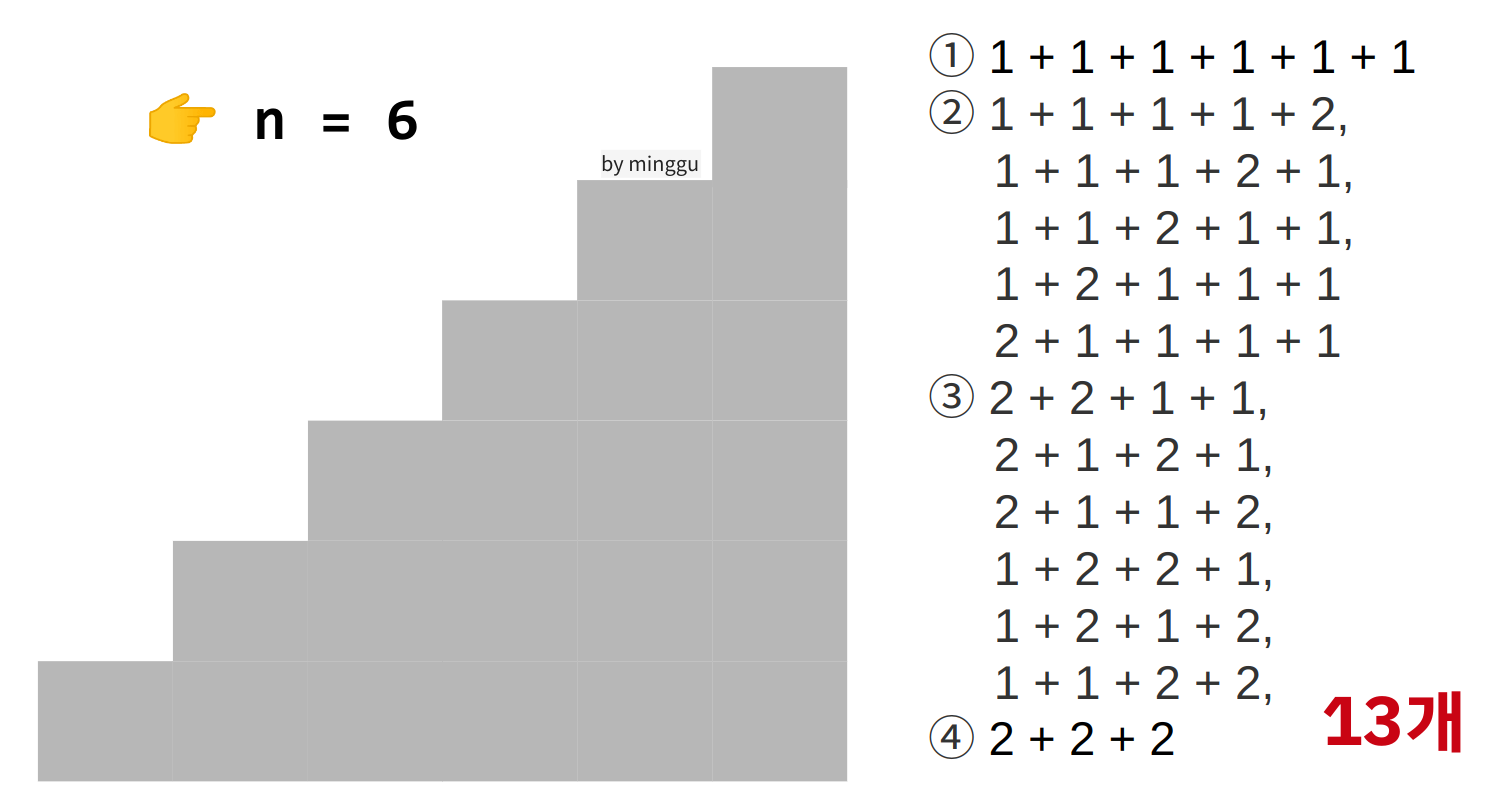
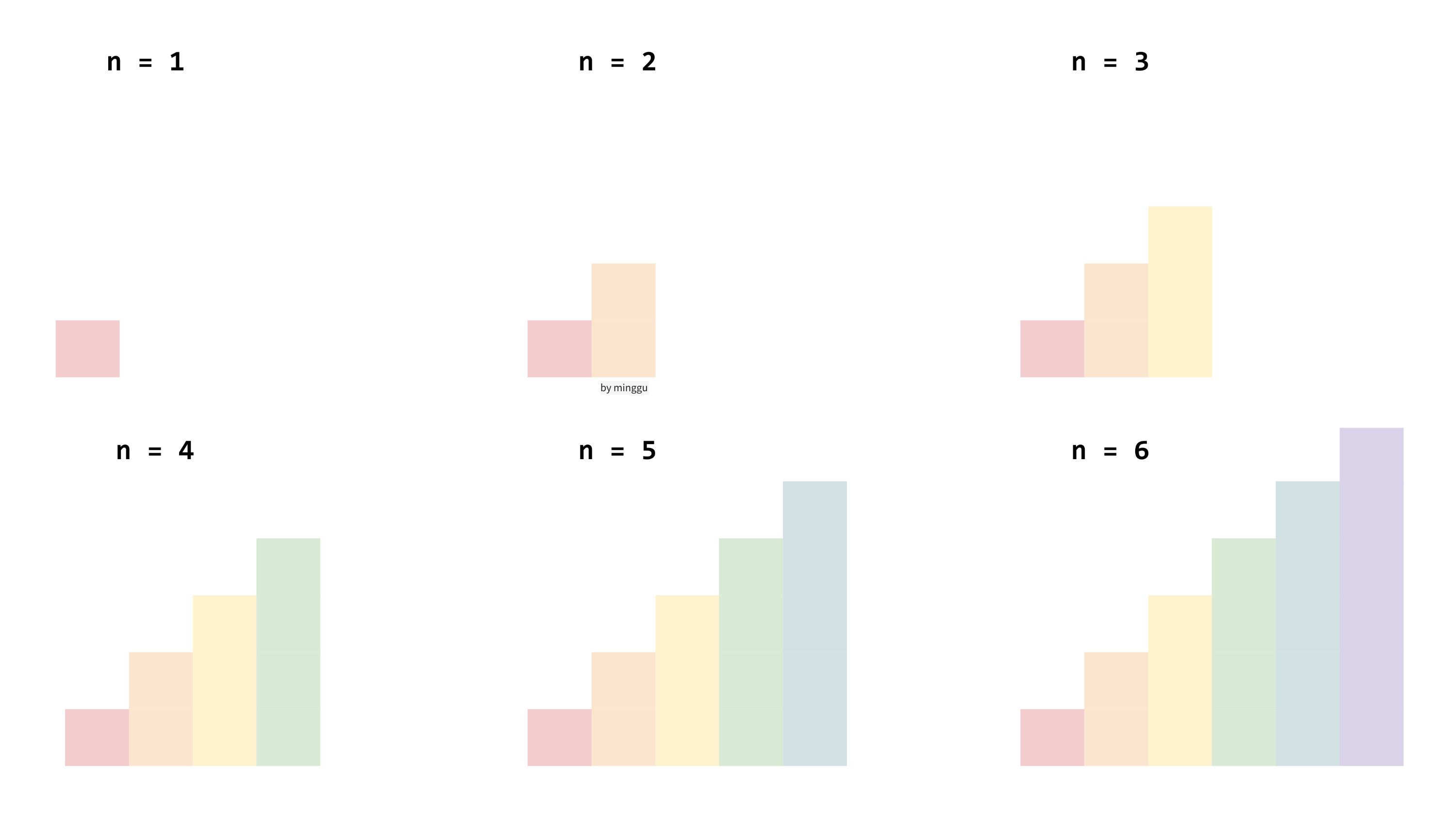
계단을 나열해보았을 때, 이를 통해서 같은 문제가 계속해서 반복된다는 것을 알 수 있다.
따라서 이 문제는 Dynamic Programming을 이용하는 문제이다.
Dynamic Programming?
큰 문제를 작은 문제로 나누어 푸는 문제로, 작은 문제가 반복된다.
(분할정복은 큰 문제를 해결하기 어려워 작은 문제로 나누어 품)
조건 : 작은 문제가 반복이 일어남. 같은 문제는 구할 때마다 정답이 같음!!
🔍Approach
그렇다면 dp에 어떤 값을 저장해야 할까?
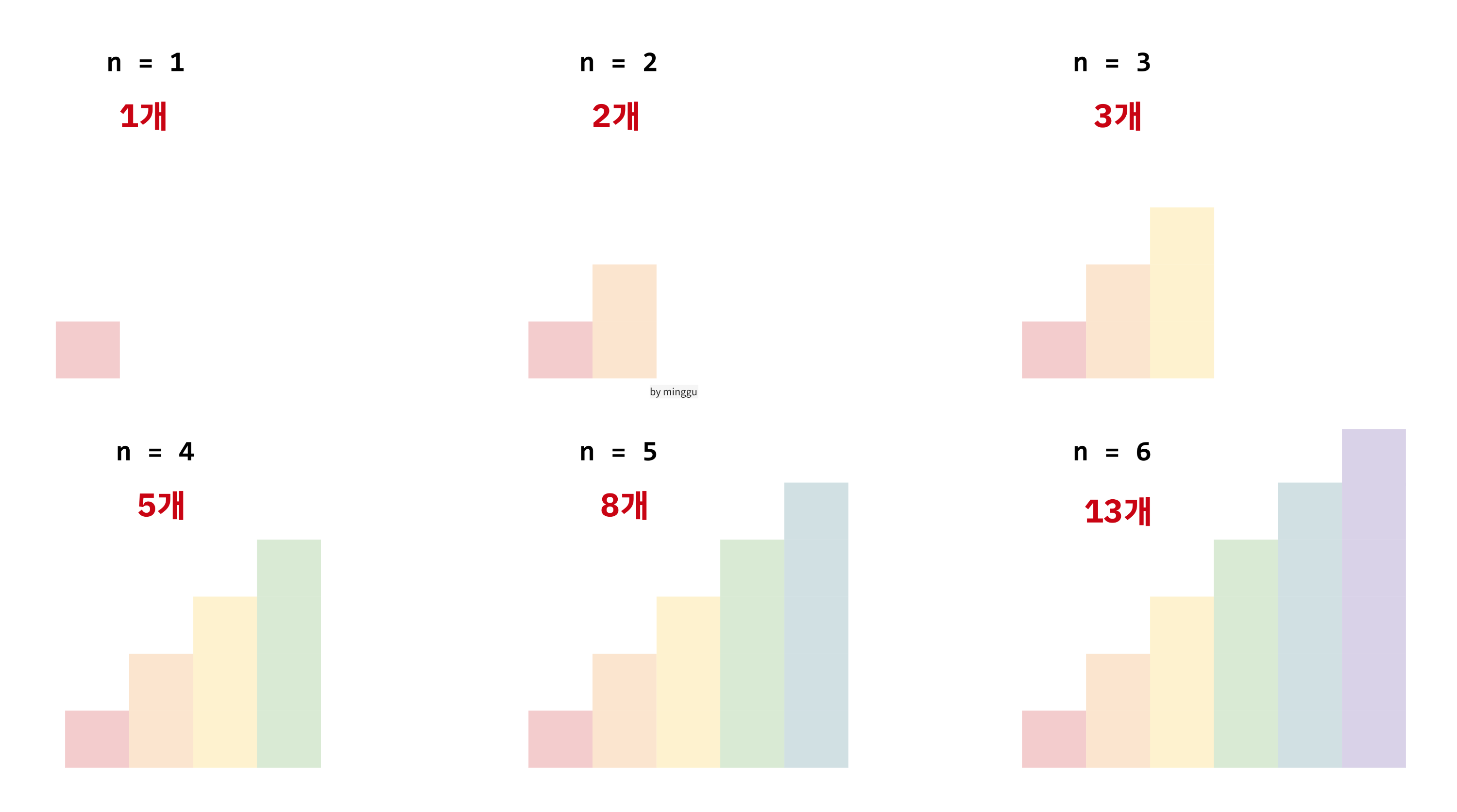
또한 n=6일 때의 경우의 수는 이전 n=1 부터 n=5일 때까지의 경우의 수가 누적되어 사용된다는 것도 알 수 있다. 또한 그림으로는 만들지 않았지만 n=0 즉, 계단이 없는 경우에도 방법은 1개 밖에 없다.
따라서, 아래와 같이 정리할 수 있다.
- n = 0일때, 1개
- n = 1일 때, 1개
- n = 2일때, 2개
- n = 3일때, 3개
- n = 4일때, 5개
- n = 5일때, 8개
- n = 6일때, 13개
…
여기서 규칙이 보이지 않는가?
⇒ n일 때의 값은 이전 값들을 더한 합으로 구해진다.
dp라는 DP 테이블에 꼭대기까지 가는 경우의 수를 저장한다고 한다고 해보자.
그러면, n = 6일때는 n = 4일 때와 n = 5일때의 값을 더하므로, dp[n] = dp[n-1] + dp[n-2]로 점화식을 표현할 수 있다.
점화식 : dp[n] = dp[n-1] + dp[n-2]
이때 주의해야 할 것은 반복문 내에서 dp[n-2]를 사용하려면 for 문의 시작 범위를 2부터 시작하도록 수정해야 한다.
또한, 이를 위해서는 dp[0]과 dp[1]은 미리 값을 넣어주어야 한다. n = 0, n = 1인 경우는 경우의 수도 오직 1개 밖에 없기 때문이다. 따라서, return해줄 때에도 n = 0이나 1일 경우는 바로 return을 1로 해주도록 예외를 두어야 한다.
만약 예외를 두지 않는다면, 아래와 같은 일이 발생한다..ㅎ
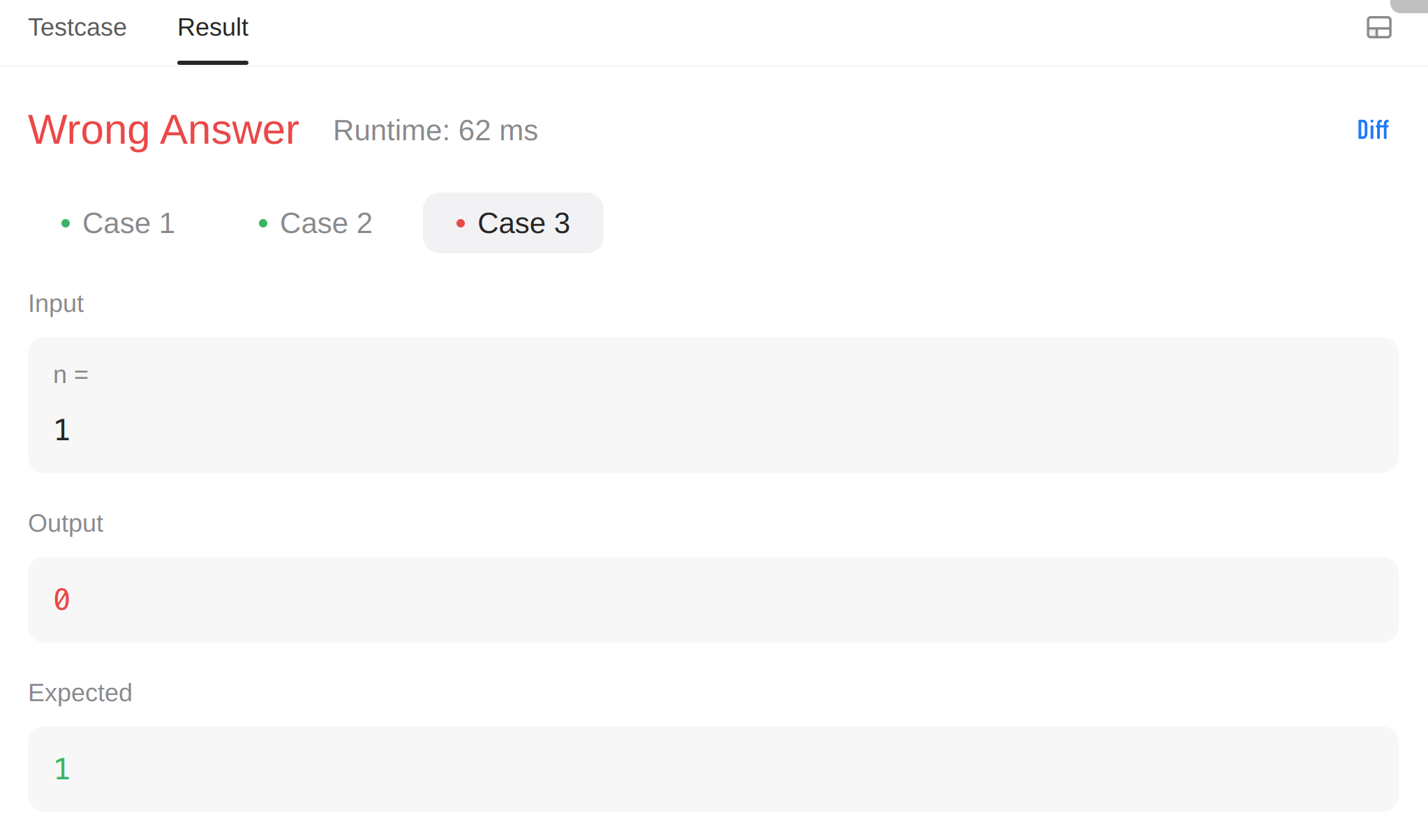
👉Flow
- 계단을 오르는 경우의 수를 저장하는 n+1크기의 dp 테이블(dp)을 만든다.
- 이때, n = 0이거나 n = 1인 경우에는 계단을 오르는 방법이 1개 밖에 없기 때문에 1로 초기화한다. 또한 이 경우에는 바로 1을 return한다.
- 이후, 2부터 n까지 반복한다. 이전 계단들의 값들을 더해가면서 dp에 저장한다. (dp[i-1] + dp[i-2])
- 이렇게 하면, dp[n]에 n개의 계단을 오르기 위한 방법의 수가 모두 저장되어 있으므로, dp[n]을 return한다.
class Solution:
def climbStairs(self, n: int) -> int:
dp = [0] * (n+1)
dp[0] = dp[1] = 1
if n == 1 or n == 0:
return 1
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]🚩My submission
class Solution:
def climbStairs(self, n: int) -> int:
dp = [0] * (n+1)
if n == 1:
dp[n] = 1
else:
dp[1] = 1
dp[2] = 2
for i in range(3, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
풀리긴한데,, dp[0]을 1로만 수정해준다면, 좀 더 나은 코드로 바꿀 수 있다. 아래처럼!
class Solution:
def climbStairs(self, n: int) -> int:
dp = [0] * (n+1)
dp[0] = dp[1] = 1
if n == 1 or n == 0:
return 1
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
- Time Complexity: O(n)
- Space Complexity : O(n)
🚩Others submission
class Solution {
public:
int climbStairs(int n) {
if(n<=2)
return n;
vector<int> dp(n+1);
dp[0]=0;
dp[1]=1;
dp[2]=2;
for(int i=3;i<=n;i++)
dp[i]=dp[i-1]+dp[i-2];
return dp[n];
}
};이 분은 내가 맨 처음에 짠 코드랑 똑같다.. ㅋㅋ
🎯 Solutions Top 1 게시글
🖍Approach 1: Recursion
이 문제를 해결하기 위해서, Recursion으로 접근한다면, 피보나치 수 개념을 사용한다. n-1 그리고 n-2 계단을 위해 climbStairs 함수를 재귀적으로 호출하여, 계단을 오르는 방법의 수를 계산한다.
하지만, 이 방법은 중복된(redundant) 연산 때문에, 시간 복잡도가 O(2^n) 이된다.
class Solution:
def climbStairs(self, n: int) -> int:
if n == 0 or n == 1:
return 1
return self.climbStairs(n-1) + self.climbStairs(n-2)/- Time complexity : $O(2^n)$
역시나 이 방법은 실제로 코드를 돌려보면 시간 초과가 뜬다.

🖍Approach 2: Memoization (메모이제이션)
메모이제이션 해결책은 도입하여 불필요한(redundant) 계산을 피하는 memoization을 사용함으로써 재귀법을 향상시켜준다.
- 이 풀이는 각 step n에 대한 미리 계산된 결과를 저장하기 위해 정렬되지 않은 map(memo)을 사용한다.
- 재귀호출을 하기 전에, 주어진 n 에 대한 결과가 memo 맵에 있는지 확인한다.
- 만약에 있다면, 저장된 값을 return한다.
- 만약 없다면, 결과를 재귀적으로 계산하고, 나중에 참고할 수 있도록 memo안에 저장한다.
class Solution:
def climbStairs(self, n: int) -> int:
memo = {}
return self.helper(n, memo)
def helper(self, n: int, memo: dict[int, int]) -> int:
if n == 0 or n == 1:
return 1
if n not in memo:
memo[n] = self.helper(n-1, memo) + self.helper(n-2, memo)
return memo[n]- Time Complexity: 메모이제이션을 활용하면 각 계단 수에 대한 해답은 한 번만 계산되고 메모에 저장되기 때문에 O(n) (최악의 경우, $O(2^n)$)
- Space Complexity : O(n)
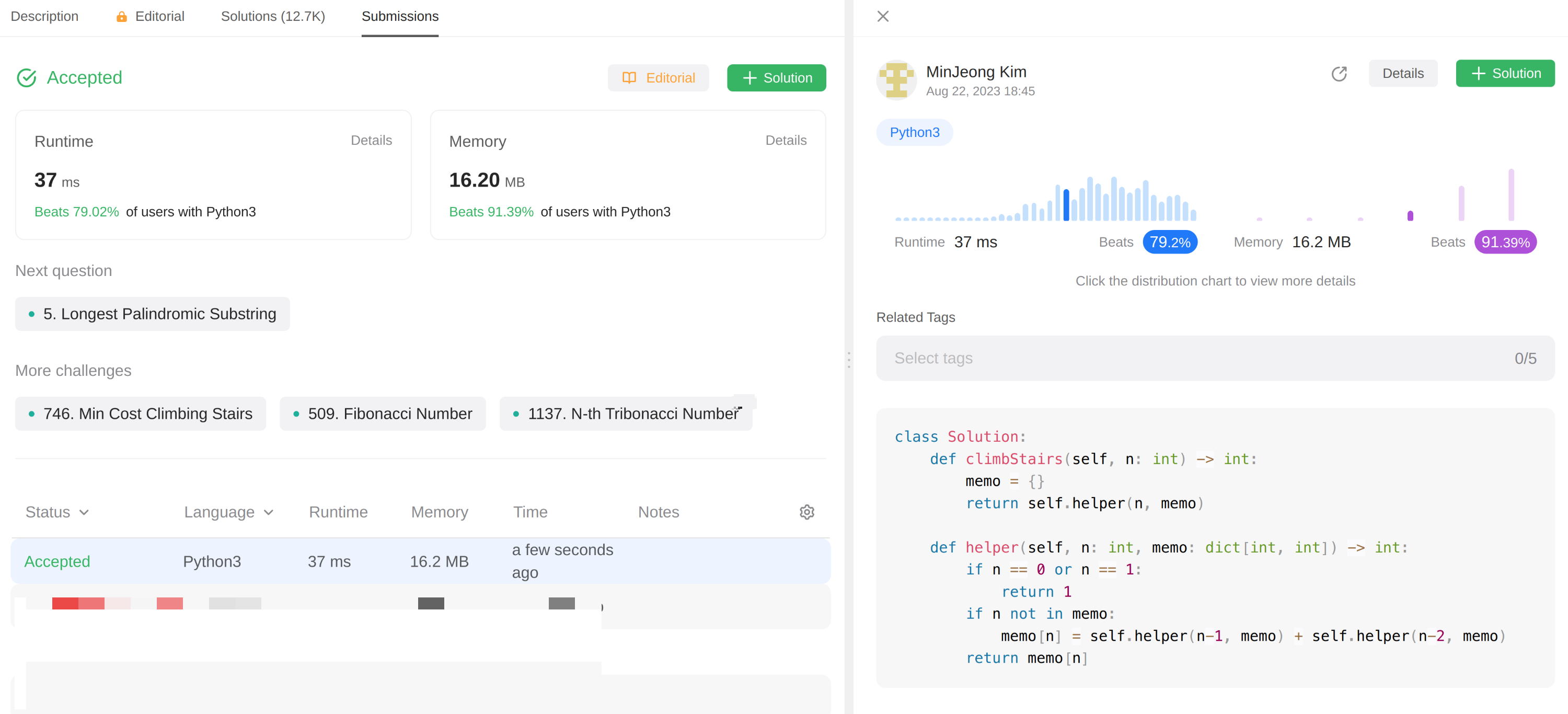
🖍Approach 3: Tabulation 테이블화 (→ DP)
표를 이용한 방법은 재귀호출을 제거하고, 문제를 반복적으로 해결하기 위해 bottom-up방식을 사용한다.
- 이 방식은 각 계단을 오르기 위한 방법의 수를 저장하기 위해, n+1 크기의 DP 테이블(dp)을 만든다.
- 이 계단을 오르기 위해서는 오직 한 가지의 방법밖에 없기 때문에, 기본적인 경우(0 and 1 steps)는 1로 초기화한다.
- 그리고 나서, DP테이블을 2부터 n까지 반복하면서, 이전 2 계단을 이용하여 값들을 더해가면서 DP table을 채운다.
- 마지막으로, DP 테이블의 가장 마지막 index 값에 있는 값을 return한다. 이는 꼭대기에 이르는 총 방법의 수를 나타내기 때문이다.
class Solution:
def climbStairs(self, n: int) -> int:
if n == 0 or n == 1:
return 1
dp = [0] * (n+1)
dp[0] = dp[1] = 1
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]⇒ 내가 한 풀이와 거의 비슷하다. 위에서 바로 return해주는 점이 차이이다.
- Time Complexity: O(n)
- Space Complexity : O(n)
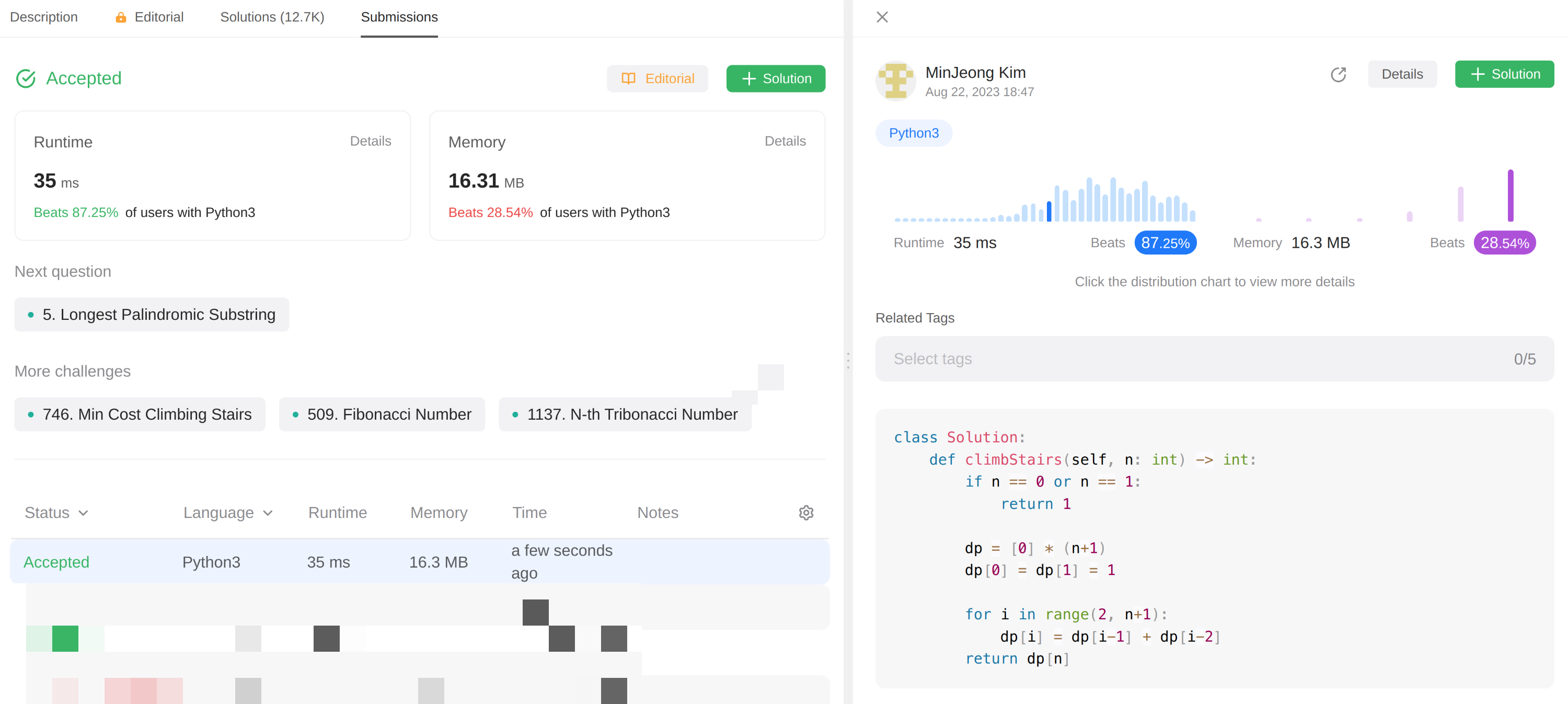
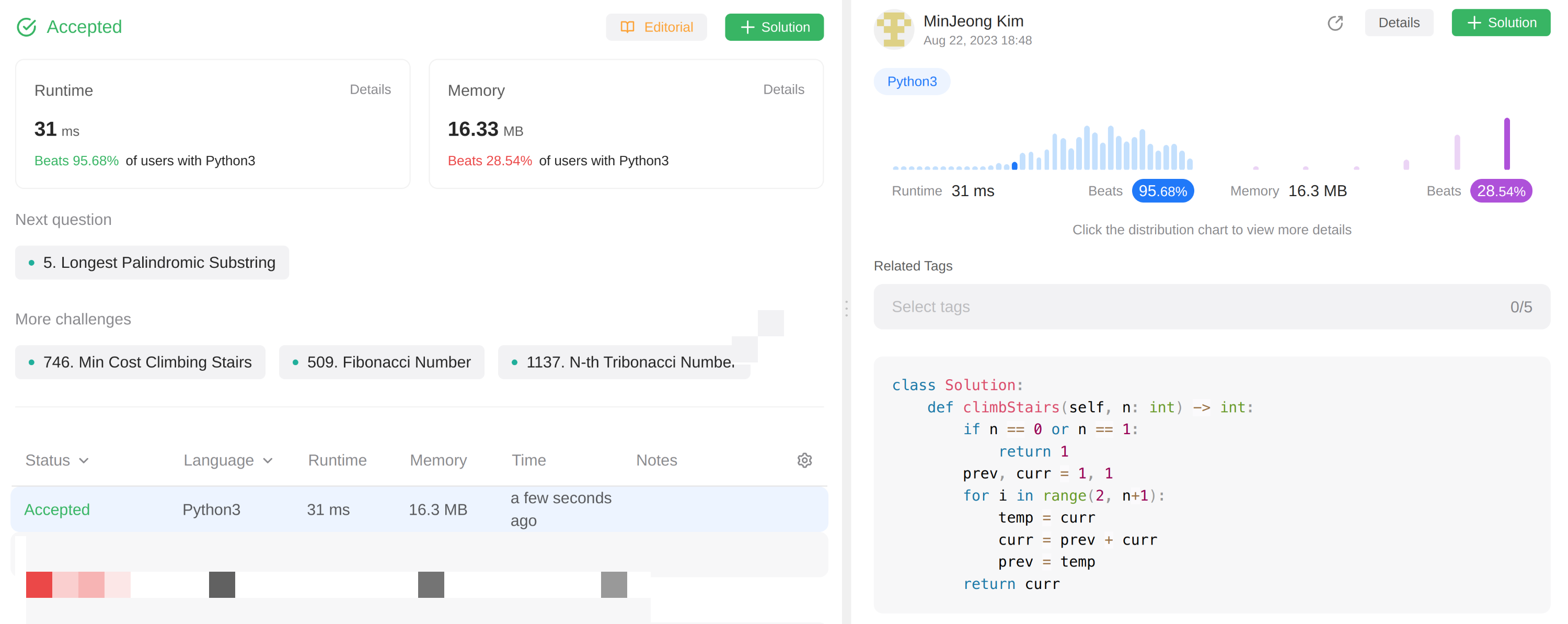
🖍Approach 4: Space Optimization 공간 최적화
공간 최적화 해결책은 DP 테이블 대신에 오직 2가지 변수(prev, curr)만을 사용하여 공간 복잡도를 훨씬 더 줄여준다.
- 기본적인 경우(0 and 1 steps)에 이르는 방법은 오직 1가지이기 때문에 prev와 curr는 1로 초기화한다.
- 그리고 나서 각각의 반복에서, 그들의 값을 옮기면서(shifting) prev와 curr을 업데이트해준다.
- curr는 이전 2가지 변수의 합이 되고, prev는 curr의 이전 값을 저장한다.
class Solution:
def climbStairs(self, n: int) -> int:
if n == 0 or n == 1:
return 1
prev, curr = 1, 1
for i in range(2, n+1):
temp = curr
curr = prev + curr
prev = temp
return curr- Time Complexity: O(n)
- Space Complexity : O(1)
💡TIL
- DP문제인데 금방 규칙성이 발견되어, 쉽게 풀 수 있었던 것 같다. 혹시나 꼬인 문제일까 하여 어려운 방식으로도 접근했지만 꼬인 문제는 아니었다.. 혹시나 해서 바로 코드로 옮겨보길 잘한 것 같다. 내 풀이가 맞을줄은 몰랐는데 대표적인 dp방식으로 풀이한 것 같다.
- 풀고 나서 dp방식 말고 다양한 방식으로 풀 수 있는 점을 배울 수 있었다.
- DP로만 접근하려고 했는데, DP 리스트가 아니라 변수 2개를 이용해서 더 효율적으로 바꿀 수 있다는 점을 배워간다. 정말 간단한 방법이었는데 이에 대한 아이디어를 얻지 못했던 것 같다. 다음에 계단과 관련된 비슷한 문제를 풀게 되면 꼭 활용해야겠다.
'🧑💻Problem Solutions > LeetCode' 카테고리의 다른 글
| #917. Reverse Only Letters (Python/파이썬) (2) | 2023.10.10 |
|---|---|
| [LeetCode] #101. Symmetric Tree (Python/파이썬) (2) | 2023.09.01 |
| [LeetCode] #15. 3Sum (Python/파이썬) (5) | 2023.08.09 |
| [LeetCode] 94. Binary Tree Inorder Traversal (Python) (0) | 2023.08.07 |
| [LeetCode] #167. Two Sum 2 (Python) (0) | 2023.07.25 |



